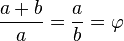Hace días terminé de leer El hombre que calculaba, la historia fascinante de un calculista llamado Beremís. Este libro, que es una suerte de anecdotario sobre las aventuras de un calculista que sale favorecido y bien librado de muchos problemas y disyuntivas gracias a su comprensión de lo que nos rodea como un todo matemático. Una de esas anécdotas es la que quiero compartir con ustedes, y es sobre cómo la belleza también podría tener una razón matemática.
Todo comienza cuando un hombre le plantea al calculista una inquietud, y es que este hombre quiere pedir en matrimonio a una mujer a la que no puede ver, pero quiere saber si ella es hermosa o no, y pregunta a Beremís si es posible determinarlo sin observar a la mujer. Entonces el hombre que calculaba solo pidió a la mujer que midiera ciertas partes de su rostro para obtener así los datos necesarios para "la fórmula matemática de la belleza"
¿Es posible saber en qué consiste esa fórmula matemática de Belleza?
Nada más fácil. El calculista Beremís, explica una relación curiosa, de un modo elemental y simple.

Dada cierta magnitud AB (representada en este caso por un segmento de recta), podemos dividirla al medio, o en dos partes desiguales. La división en dos partes desiguales puede ser hecha, es claro, de una infinidad de maneras diferentes.

Entre las divisiones de AB en partes desiguales, ¿habrá alguna preferible a las otras?
- Sí –contesta el matemático-. Existe una manera “simpática” de dividir un todo en dos partes desiguales. Veamos en qué consiste esta forma de división.
Consideremos el segmento AB dividido en dos partes desiguales.
Admitamos que esas partes desiguales representen la siguiente relación:
La proposición es la siguiente:
segmento total : parte mayor = parte mayor : parte menor
Esa división corresponde a la forma simpática que pueden presentar las dos partes desiguales. Podemos formular la siguiente regla:
“Para que un todo dividido en dos partes desiguales parezca hermoso desde el punto de vista de la forma, debe presentar entre la parte menor y la mayor la misma relación que entre ésta y el todo.”
En el rostro femenino “matemáticamente” hermoso, la línea C de los ojos divide a la medida total AB, en media y extrema razón.
|

Podemos llamarla también división en media y extrema razón.
Es fácil observar que el título puesto por el calígrafo en la primera página de una obra divide, en general, la medida total del libro en media y extrema razón.
La división áurea es observada, con admirable nitidez, en las fachadas de los edificios que se distinguen por la perfección de sus líneas arquitectónicas. El famoso “panteón” de París, representado en la figura, es un ejemplo notable. Siendo AB la altura del monumento, el “punto de oro” se destaca de manera inconfundible; es el punto C por el que pasa, ya sea la línea de la base del frontispicio, o el plano que corta la base de la cúpula.
 |
Lo mismo sucede con la línea de los ojos, que divide, en las personas bien proporcionadas, la medida total del rostro en media y extrema razón. Se observa también la divina proporción en las partes en que las falanges dividen los dedos de la mano. La división en media y extrema razón se puede hallar también en la Música, en la Pintura, en la Escultura y en la Arquitectura.
En la división áurea la relación entre el todo y la parte mayor, es igual, más o menos, a:
esto es siempre,
809 / 500
809 / 500
En las líneas principales del rostro femenino “matemáticamente hermoso” resulta constante aquella relación.
-----
Tomado de: El Hombre que Calculaba, de Malba Tahan.
Otros enlaces relacionados con el número de oro y la proporción áurea: